Bentornato su Capitalmente, spesso in finanza si parla di rendimenti “medi”, ma in pochi conosco la differenza tra media aritmetica e media geometrica dei nostri investimenti.
Siamo alla fine dell’anno e si sprecano le previsioni sull’andamento di mercato dei prossimi anni.
In tanti sostengono che l’S&P500 sia “sopravalutato”, Goldman Sachs ad esempio fa la triste previsione di un rendimento medio nominale per i prossimi 10 anni del 3%.
Ammesso e concesso che abbia ragione, la media indicata è quella aritmetica che è diversa da quella geometrica che si applicherà ai tuoi investimenti.
Andiamo però con ordine e vediamo di scoprire insieme la differenza tra media aritmetica e media geometrica anche con l’ausilio del foglio Excel che alla fine potrai scaricare.
La media aritmetica
La media aritmetica è la somma di una serie di numeri divisa per la quantità di numeri nella serie.
È il tipo di media più comune e viene spesso utilizzata per calcolare velocemente il rendimento medio di un investimento su un periodo di tempo.
Immagina di avere un portafoglio di investimenti che ha reso il 5% il primo anno, il 10% il secondo anno e il 15% il terzo anno.
La media aritmetica del rendimento sarebbe:
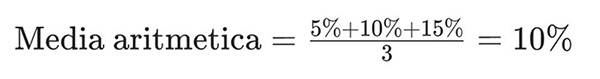
Pensa alla media aritmetica come alla velocità media di Flash (il supereroe dei fumetti) durante una corsa.
Se Flash corre a 100 km/h per un’ora, poi a 200 km/h per un’altra ora e infine a 300 km/h per un’ultima ora, la sua velocità media sarebbe 200 km/h.
Non tiene conto delle variazioni di velocità, ma solo della media delle velocità.

La media geometrica
La media geometrica è la radice n-esima del prodotto di n numeri.
È particolarmente utile negli investimenti perché tiene conto dell’effetto della capitalizzazione composta.
Utilizzando lo stesso esempio di prima, per calcolare la media geometrica dei rendimenti del 5%, 10% e 15%, si procede così:
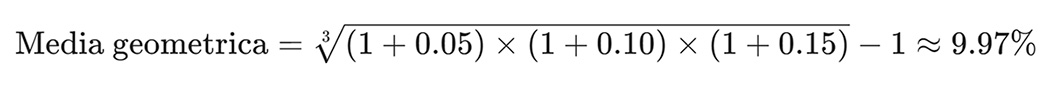
Immagina la media geometrica come il viaggio nel tempo di Doctor Strange, ogni salto temporale (o rendimento annuale) influenza il successivo in modo esponenziale.
Se Doctor Strange viaggia nel tempo e modifica un evento, questo cambiamento si ripercuote su tutti gli eventi futuri, proprio come la capitalizzazione composta influenza i rendimenti futuri.
Un esempio pratico per capire la differenza tra media aritmetica e media geometrica
Per capire meglio la differenza prendiamo il rendimento in Euro del S&P500 dal 2000 in poi.
Ipotizziamo di investire 10.000 € il 1° gennaio 2000 (non consideriamo l’imposta di bollo annua dello 0,2%).
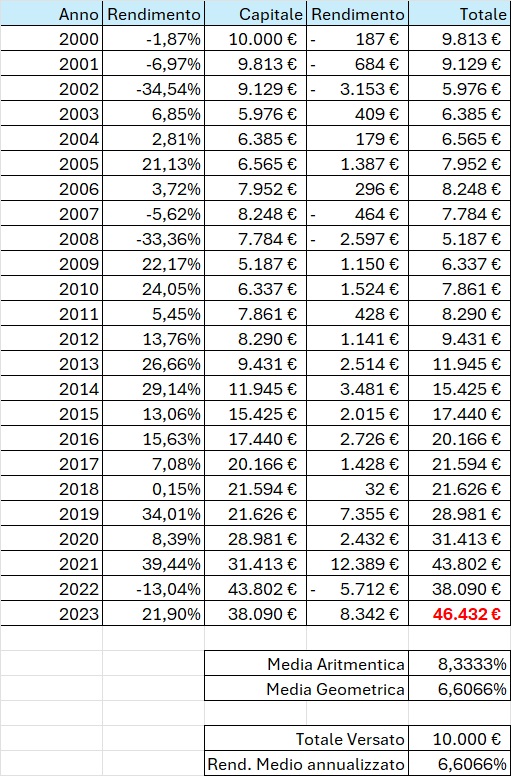
Dopo 24 anni ci troveremmo ad avere 46.432 €, la media aritmetica è pari a 8.33% e la media geometrica è 6,61%.
Un piccolo trucco per calcolare la media geometrica su Excel
In Excel per calcolare la media geometrica si usa la formula MEDIA.GEOMETRICA.
La funzione richiede che non si siano valori minuti o uguali a zero, che invece nel nostro esempio abbiamo.
Per aggirare il problema è sufficiente usarla in questo modo: MEDIA.GEOMETRICA(1+B4:B27)-1
Quindi quale è la media corretta da usare?
La media corretta da usare per calcolare il rendimento effettivo è quella geometrica, vediamo infatti come l’applicazione della media aritmetica porti ad un risultato superiore a quello reale.
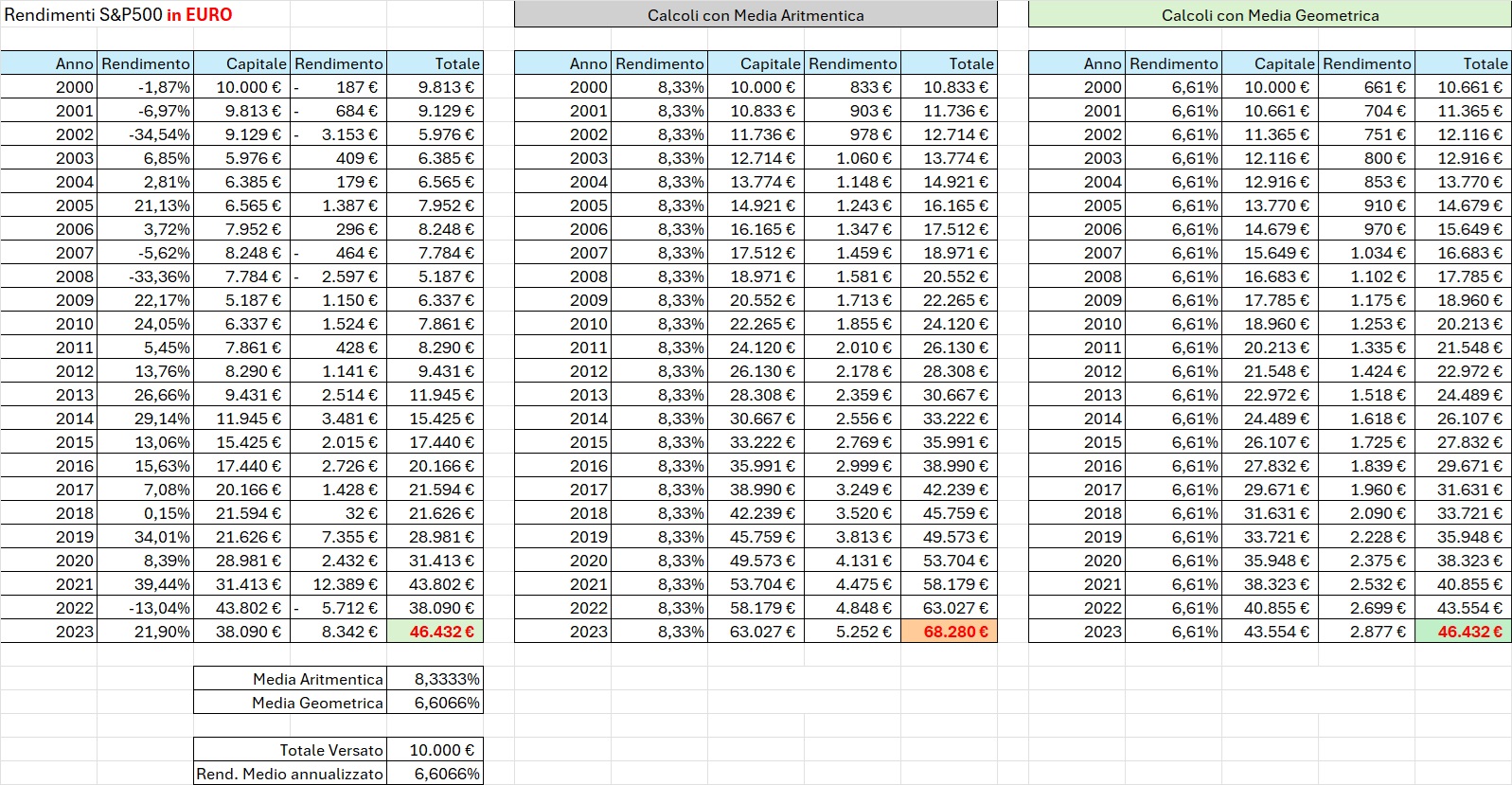
La differenza è notevole ed è dovuta alla grande differenza che hanno i rendimenti annuali che vanno da un massimo del +39.44% ad un minimo del -34.54 %.
Vi allego il link al foglio Excel utilizzato per evidenziare la differenza tra media aritmetica e media geometrica.
In conclusione la media aritmetica è “errata”?
Ovviamente la media aritmetica non è errata, essa è utile per avere una visione rapida e semplice dei rendimenti medi tenendo però in considerazione che non è una misura precisa.
Al contrario la media geometrica offre una valutazione più precisa e realistica degli investimenti a lungo termine.
Anche per oggi è tutto, se hai dubbi o suggerimenti lascia pure un commento sarò felice di risponderti, spero di rivederti presto su Capitalmente, il tuo blog di finanza personale a porta di click.
Ricordati, come sempre, che l’articolo non rappresenta una sollecitazione all’investimento ma è una mia opinione basata su dati e studi condotti nel tempo.







